Defined as a political regime in which the people rule, populism seems to be growing in many countries. However, opinions on populism often ignore a basic question: who is “the people”? Over the past 50 years, economists and political scientists have demonstrated that “the people” as a governing agent does not exist. Although the topic may appear abstract or theoretical, it has momentous practical implications for how to interpret election (or referendum) results.

The reality is that “the people” does not exist except as a collection of individuals with different preferences and values. Only on very few issues (a minimum of public order, for example) is there presumptive agreement among all members of a society. Should more milk or more cars be produced, and in which quantities? Who should earn more? On such questions, it is difficult to find many individuals sharing the same opinion. Saying that the people should rule or govern thus means, in practice, that a subset of the people will rule over another subset of individuals whose preferences and values will be violated.

The elusive will of the people 

People (the individuals who make up “the people”) can govern through elections (including referendums). However, it has been shown that voting results do not represent what “the people” wants. The results can be as incoherent as if “the people” are irrational. This fact was first discovered by Nicolas de Condorcet, an 18th-century French philosopher and mathematician, and has since been the object of many mathematical confirmations and elaborations. It is called the “Condorcet paradox” or the “paradox of voting.”

To illustrate, consider an electorate composed of three voters, Voter 1, Voter 2, and Voter 3; and three policy options, X, Y, and Z (such as, for example, an employment subsidy, increased family allocations, and a higher minimum wage). Table 1 shows the hypothetical preferences of the three voters. Voter 1 prefers X to Y and Y to Z; hence his ordering can be represented as “X Y Z.” If this voter is coherent or rational, he prefers X to Z—that is, his preferences are assumed to be “transitive.” Voters 2 and 3 have different preferences, which are also transitive.

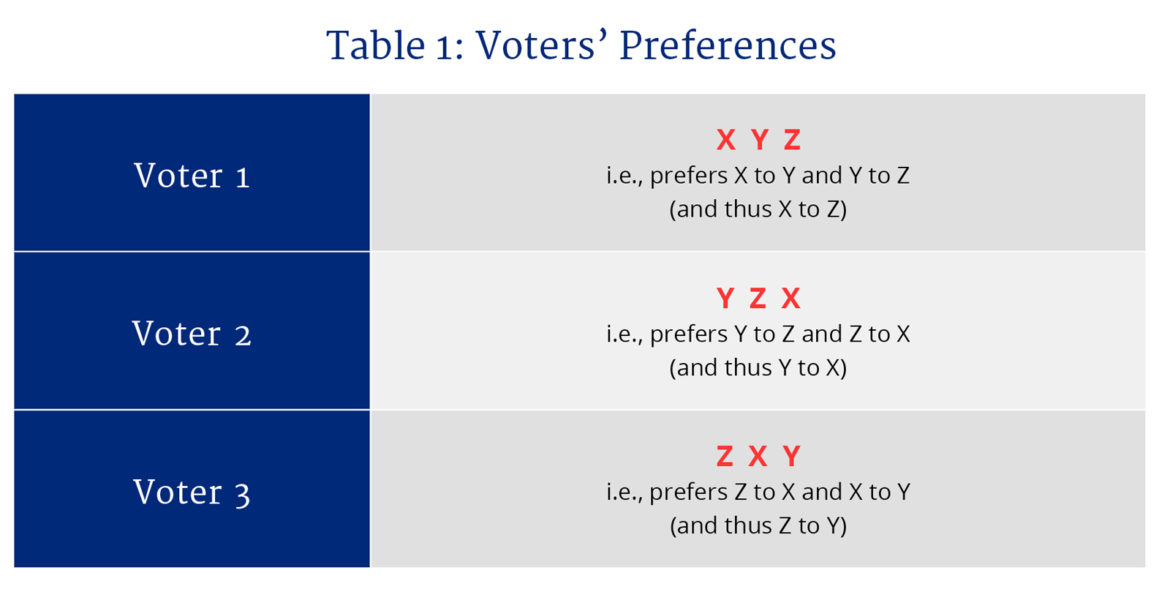
Now suppose that the three voters are asked to choose between X and Y. Given their preferences, it is easy to see that X will win with two-thirds of the vote because both Voter 1 and Voter 3 prefer X to Y (see Table 2). If the choice is between Y and Z (perhaps in a subsequent election), Y will win. But if the alternative presented to the voters is between Z and X, it is Z that will win. The electorate prefers both X to Z (as the first two elections imply, through the transitivity property) and Z to X—a clear contradiction.

Despite each individual voter being rational, the aggregation of their votes is not. An incoherent majoritarian cycle will occur even if no voter changes his or her mind. We cannot know what “the people” wants. “The people” does not exist as a rational chooser.

If we modify the hypothetical preferences of our three voters, certain configurations will avoid the Condorcet paradox. However, the more voters there are, the more likely the paradox will mar voting results.

One empirical confirmation of this phenomenon was observed over seven days in January 1925. With only one senator changing his mind (or being incoherent), the U.S. Senate voted to refer a hydroelectric project to a study commission (X) instead of allowing private development (Y); to support private development (Y) instead of public ownership (Z); and then, finally and inconsistently, to approve public ownership (Z) instead of a study commission (X).

It would not be surprising if, as in the old jest, the Quebec electorate once literally favoured (and perhaps still favours) “an independent Quebec in a united Canada,” even if each individual voter had coherent preferences.

A crucial discovery was made when Kenneth Arrow, then at Stanford University, mathematically demonstrated that the Condorcet paradox generalizes to all voting methods that respect a small number of simple axioms (such as transitivity of individual preferences, non-dictatorship, and independence of irrelevant alternatives). He later won a Nobel Prize in economics. To simplify, Arrow’s “Impossibility Theorem” established that the result of a vote is either irrational (somewhat like in the Condorcet paradox) or dictatorial in the sense that one individual’s preferences win, whatever other individuals’ preferences are.

Thus, the people cannot rule. You either have an irrational people (in the aggregate) who rule, or else a dictator (of the right or the left) who claims to embody the so-called “will of the people.” To feed the illusion that there is one unified people, a populist leader has to find “enemies of the people” that are defined out of the people he claims to represent. History provides multiple illustrations of this.

Other problems exist as well. Notably, different voting methods can produce different results. So, too, can control of the agenda to determine which alternatives are put before voters.

What democracy is good for

There is one sense in which populism would be possible: if it is defined as a political regime in which, as much as possible, each individual citizen governs himself—“self-government” literally. However, there is already a label historically associated with such a political philosophy: classical liberalism, as represented by theorists of limited government such as Adam Smith, Jean-Baptiste Say, Milton Friedman, Friedrich Hayek, James Buchanan, and many others.

Populism as commonly and historically understood is an exaggeration and corruption of democracy. Democracy is a good way of changing the political personnel in government. But it does not say anything about what “the people” wants; it just reveals whether a majority, the current one, is or is not satisfied with the current government. This is useful enough, and this is the democracy that is realistically possible.

On November 18, Professor Zhang Weiwei appeared in Toronto via zoom for an interview from Shanghai to give China’s perspective on how the world sees his country. Dr. Weiwei is an eminent dean of the China Institute at Fudan University in Shanghai and a personal advisor to President Xi.  The transcript of that interview with The Hub’s executive director Rudyard Griffiths is posted here. 

I was there and here are my thoughts on that evening’s conversation.

What China has done in the past 40 years is unique in human history. It has gone from a peasant agricultural country to a global economic superpower with an economy as big or bigger than the US, depending on how you measure GDP. China virtually eliminated poverty and now has a middle class of 400 million people. For the past decade it has been strutting the globe, buying up resources, and muscling its way on the world stage. And the picture isn’t pretty. China is now the world’s biggest producer of carbon dioxide, accounting for half of new emissions. It’s opening coal-firing plants by the hundreds. It’s a growing threat to its neighbours, unapologetic about stealing trade and intellectual property, a serial violator of human rights, and is now on the verge of entering a cold war with the U.S. 

Professor Zhang Weiwei is an intelligent, scholarly, thoughtful, and soft-spoken spokesman. According to his hour-long interview, we in the West have a distorted view of the professor’s country and he wants to set us straight. Not only is China not an authoritarian nation, but Dr. Weiwei points to Pew surveys that show 80 to 95 percent of Chinese believe China is moving in the right direction. The professor is being modest; usually in dictatorships that number hovers closer to 100 percent. For China, government is a necessary virtue while in the West a necessary evil. Anyone who thinks Chairman Mao, Deng Xiaoping, or President Xi Jinping are authoritarian is “a little bit lazy in their thinking” especially the political scientists in the West who practice what he calls a “pseudoscience” taught in Western elite universities. Here he has a point. With the influence of postmodernism, our universities are rebelling against rationalism. 

He goes on to say that China is a meritocracy, unlike the West where privilege counts. The Chinese admire those who strive from the bottom as President Xi. On religion, he says China has a more inclusive tradition welcoming all religions, whereas the West excludes religions. I looked to see if he said this with a straight face; he did. China’s communist party also has a “holistic” approach to government, considering the needs of all the people, not just the rich as they do in the U.S. The jailing of high-tech executives and repression of Hong Kong must be fake news perpetrated by a lazy media following orders from Washington. On the threat of conflict with the U.S., Professor Zhang says that over the past 242 years, the U.S. has had only 16 years of peace while China has not fired a shot in the past four decades; they let the North Koreans and Vietnamese do the shooting for them. I thought he might at least be grateful to the U.S. for defeating China’s biggest threat in the Pacific in the last World War. Of course, there will be consequences if the U.S. crosses certain red lines concerning China’s national interests; Taiwan for instance. 

He was thankful for the release of Meng Wanzhou, with no mention of Michael Spavor and Michael Kovrig. Concerning the denial of Huawei’s participation in building 5G infrastructure in Canada, why that’s just “grossly unfair.” 

He hopes that’s all behind us now and we can cooperate and get back to business as usual so we can prosper together. On the question of prosperity, Dr. Zhang predicts that by 2030 China’s middle class will reach 800 million, over twice the size of the U.S. population. His evaluation of President Xi is very flattering: he’s intelligent, competent, and sophisticated. That last feature is surprising. We obviously have different views on the meaning of sophistication.

Finally, we come to Covid-19 and what an extraordinary job President Xi did to bring the virus under control. On January 23, 2020, President Xi locked down the city of Wuhan.  If China hadn’t taken that step, “Covid-19 would have spread across the country.” It may have stopped it in China, but so far it has killed some 30,000 Canadians and sickened almost two million. This recalls Stalin’s comment about the loss of one life being a tragedy etc.

Further thoughts going through my mind that evening:  

• The Chinese government knew about the virus in early December of 2019—some believe earlier—and kept quiet about it. They started locking people in their apartments in January of 2020, but continued flights out of Wuhan to Europe, especially to northern Italy where the virus started killing thousands, all the while pressuring countries to keep those flights coming. We complied so we wouldn’t look like crazy anti-Asian racists. The virus has so far killed over five million around the world and still the Chinese won’t let independent scientists investigate the source of the virus, insisting it started in the US; even America’s worst enemies don’t believe it. Until the Chinese come clean, China’s reputation will continue to suffer around the world. They don’t seem to care. It’s no surprise Xi stayed away from COP in Scotland. China keeps looking to charm friends, but all they have are North Korea, Cuba, Venezuela and perhaps a shifty Putin. Instead, China has forced an alliance of Australia, U.S., Japan and India—the Quad—to promote the security of the Indo-Pacific region. Even China’s neighbours are nervous. 

• On Chinese holistic approach to government, the only holistic objective I can see is the survival of the Chinese Communist Party. End of story. The party is petrified of its own people, spending more money on surveillance than on defence. With a population of 1.4 billion, it has much work on its hands monitoring and following people everywhere. Will the Chinese continue to tolerate a society that looks like Orwell’s 1984? And where’s Peng Shuai?

• On Taiwan, Xi’s prestige is on the line. He took back Hong Kong but at a high political cost internationally. Taking Taiwan is a different order of difficulty. It’s risky politically and militarily, and losing will seal President Xi’s fate. But he has reason to think the U.S. weak; an indecisive and incompetent president Biden, increasing crime and racial tensions, an economy struggling to recover from almost two years of Covid-19 disruption, a bungled military departure of Kabul, and a woke culture that’s splitting the nation socially and politically. America has looked weak before, especially after the Vietnam war, but it recovered under Reagan and the fall of the Berlin Wall. The Japanese in the 70s also thought the U.S. was finished. Yes, this time is different. It always is. Betting against the U.S. is always precarious. But President Xi is a true believer in Marx and Engels and he’s certain the West and capitalism are finished. He’s an authoritarian with a penchant for risk and that makes him dangerous; let’s hope he not reckless as well. He might be politically more insecure than we think, which might explain his aggressive behaviour. 

• China has pulled off an extraordinary economic feat over the past four decades, but 10 percent annual growth is over. Debt, both private and public, is mounting fast. Vast buildings and apartments sit empty with bridges going nowhere draining the savings of millions of investors. A real estate crash may be on the horizon. Historian Niall Ferguson estimates China’s real growth is closer to 2 to 3 percent annually. International investments are slowing along with growth and cheap labour. Demographics are also moving in the wrong direction. It’s estimated that the country’s population will drop drastically by the end of the decade.

• A growing middle class is a blessing and threat. Many have become rich—many very rich—and they want to stay that way. That’s the problem for Xi. Any effort by the government to slow growth or confiscate property or wealth has the potential to cause a political crisis as wealth moves offshore. After all, many of those 400 million—now in the bourgeois class—are also members of the CCP. A rich society also wants freedom, and many are finding it outside China. 

• Professor Weiwei may be right in his harsh analysis of political science. Twenty-five years ago, the late political scientist Harry Rowen of Stanford University predicted China would become a democracy around 2015 as it got richer. China did get richer, and so did authoritarianism. Will it last? Milton Friedman once said if you had to invest in either China or India, take India; you need freedom and capitalism for real prosperity. Not to suggest China’s long run is over, but predictions are a fool’s game. In that sense we really don’t know China. Then again, President Xi and Professor Weiwei should be a bit more modest about their knowledge of the West.